Substitution Property Of Equality Definition
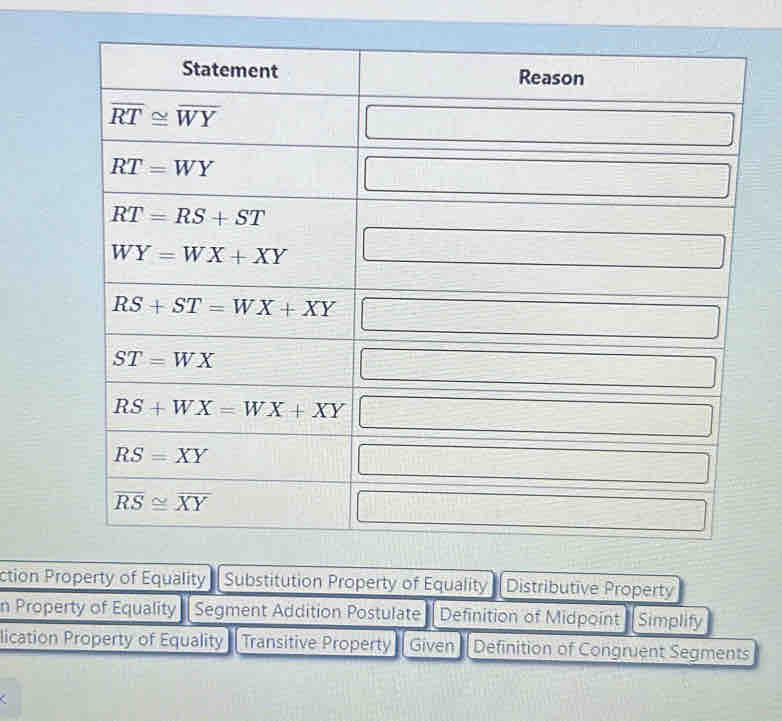
The substitution property of equality is a fundamental concept in mathematics, particularly in algebra and equation solving. It states that if two expressions are equal, then one expression can be substituted for the other in any equation or expression without changing the truth or validity of the equation. This property is essential for solving equations, simplifying expressions, and proving mathematical statements.
Mathematically, the substitution property of equality can be represented as follows:
If a = b, then f(a) = f(b) for any function f.
In simpler terms, if we have an equation a = b, we can replace a with b (or vice versa) in any other equation or expression, and the resulting equation or expression will be equivalent to the original one.
Importance of the Substitution Property
The substitution property is crucial in various mathematical operations, including:
- Solving Equations: It allows us to manipulate equations to isolate variables, making it possible to solve for unknown values.
- Simplifying Expressions: By substituting equivalent expressions, we can simplify complex algebraic expressions and make them more manageable.
- Proving Identities: The substitution property is used to prove trigonometric, algebraic, and other types of identities by demonstrating that two expressions are equivalent.
Examples of the Substitution Property
Example 1: Solving an Equation
Given the equation 2x + 5 = 11, we want to solve for x. If we know that 2x = 11 - 5 (from a previous equation), we can substitute 2x with 6 (since 11 - 5 = 6) into the original equation:
2x + 5 = 11 becomes 6 + 5 = 11, which simplifies to 11 = 11. This confirms that our substitution is valid, and we can then solve for x by dividing both sides by 2, getting x = 3.
Example 2: Simplifying an Expression
If a = b + c, then we can substitute a with b + c in the expression a^2. This gives us (b + c)^2, which can be expanded to b^2 + 2bc + c^2. This substitution helps in simplifying and manipulating algebraic expressions.
Conclusion
The substitution property of equality is a powerful tool in mathematics, allowing for the manipulation and simplification of equations and expressions. Its applications range from basic algebra to advanced mathematical proofs, making it a cornerstone of mathematical reasoning and problem-solving. By understanding and applying this property, individuals can develop a deeper appreciation for the logical structure of mathematics and improve their ability to solve complex problems.
What is the substitution property of equality used for?
+The substitution property of equality is used for solving equations, simplifying expressions, and proving mathematical statements. It allows for the replacement of one expression with another equivalent expression in any equation or expression without changing its validity.
Can you provide an example of the substitution property in solving an equation?
+For instance, in the equation 2x + 5 = 11, if we know that 2x = 6, we can substitute 2x with 6, leading to 6 + 5 = 11, which is true. This substitution helps in confirming the validity of our steps in solving for x.
How does the substitution property aid in simplifying algebraic expressions?
+If a = b + c, then substituting a with b + c in the expression a^2 gives (b + c)^2. This can be expanded to b^2 + 2bc + c^2, demonstrating how substitution can help in simplifying and expanding algebraic expressions.
